MATH 111 Calculus I \(\quad\;\;\) Instructor: Difeng Cai

1.1 Functions

Definition

• A function is a rule that assigns to each element \(x\) in a set \(D\) exactly one element, called \(f(x)\), in a set \(Q\).
• The set \(D\) is called the domain of \(f\).
• The range of \(f\) is the set of all possible values of \(f(x)\) as \(x\) varies throughout the domain.
• \(x\) is called an independent variable.
  

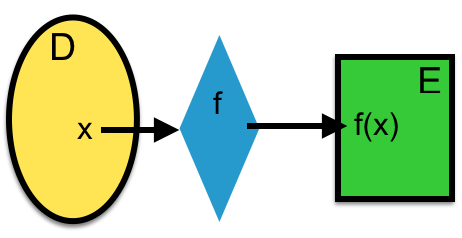
Criterion: one input ==> ONE output

Examples of functions: table representation, formula, graph, etc.

Example of function evaluation:
If \(f(x)=2x^2-x\), then \(f(a+h) = 2(a+h)^2-(a+h) = 2(a^2+2ah+h^2)-a-h=2a^2+2h^2+4ah-a-h.\)

Exercise: \(f(x) = 2x^2-x\; \text{and}\; h\neq 0,\; \text{evaluate the "difference quotient"}\; \frac{f(a+h)-f(a)}{h}.\)
Answer: \(4a+2h-1.\)

Graph of a Function

Graph of \(f\) consists of all (\(x,f(x)\)) pairs. Namely, all (input,output) pairs: \[\{ (x,f(x)) | x\in D \}.\]

Find relevant information given the graph of a function, cf. Figure 6.

The Vertical Line Test: A curve in the \(xy\)-plane is the graph of a function of \(x\) if and only if no vertical line intersects the curve more than once. (Recall the criterion: one input ==> ONE output)

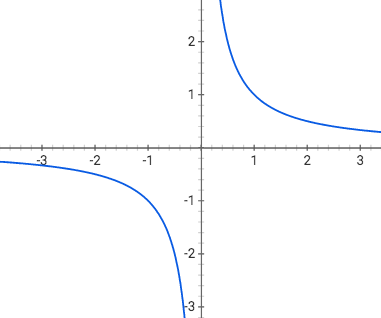
Exercise: See the x-y plot below. Is the curve(blue) a graph of a function?
Answer: yes.

Example. Plot \(x=y^2-2.\) See Figure 14(a). Is it a graph of a function? Answer: no.

Exercise: Is \(y\) a function of \(x\)? (a). \(y=x^2+2\); (b). \(y^2=x+2\)
Answer: (a) yes; (b) no.

Domain and Range

• Given a graph of \(f\), determine domain and range of \(f\):
  domain: "shaded" parts on \(x\)-axis; range: "shaded" parts on \(y\)-axis. See figure below.

• Domain Convention: Given formula of a function \(f(x)\) and the domain is not stated explicitly, the domain is the set of all numbers for which the formula makes sense and defines a real number.

  Exercise: Determine the domain and range of a function.
  (a). \(f(x)=\sqrt{1-2x}\) \(\quad\) (b). \(f(x)=\sqrt[3]{1-2x}\) \(\quad\) (c). domain of \(f(x)=\frac{1}{x^2-x}.\)
  Answer: (a). domain: \(x\leq \frac{1}{2}\); range: \([0,\infty)\).
  (b). domain: \(-\infty<x<\infty\); range: \((-\infty,\infty)\).
  (c). domain: \(\{x\; |\; x\neq 0,\; x\neq 1\}\) or in interval notation: \((-\infty,0)\cup(0,1)\cup(1,\infty)\).

  See (p.19) 7--10, 31--37 for more problems.

Piecewise Defined functions

Piecewise Defined functions: Functions that are defined by different formulas in different parts of their domains.

Examples(sketch the graphs of the functions below)

1. \(f(x) = \begin{cases} 1-x & \text{if}\;\; x\leq -1\\ x^2 & \text{if}\;\; x > -1 \end{cases} \)

2. \(f(x)=|x|\)

Even and Odd Functions

• \(f\) is an even function if \(f(-x)=f(x)\) for every \(x\) in its domain.
• \(f\) is an odd function if \(f(-x)=-f(x)\) for every \(x\) in its domain.

Excersies: even or odd or neither? \(\quad f(x)=x^3+x, \quad g(x)=x^2+x, \quad h(x)=\frac{x^4}{x^2+5}\)
Answer: \(f\) is odd, \(g\) is neither, \(h\) is even.

See (p.23) 73--78 for more exercise.

Increasing and Decreasing

\(f\) is increasing on an interval \(I\) if \(f(x_1)<f(x_2)\) whenever \(x_1<x_2\) in \(I\). (graph: an up-going curve)
\(f\) is decreasing on an interval \(I\) if \(f(x_1)>f(x_2)\) whenever \(x_1<x_2\) in \(I\). (graph: a down-going curve)

Textbook Exercises

p.19 3, 4, 7--10, 27--37, 73--78