MATH 111 Calculus I \(\quad\;\;\) Instructor: Difeng Cai

2.8 The Derivative as a Function

Derivative of \(f\)

We learned last time that the derivative of \(f\) at \(a\) is defined by \[f'(a) = \lim_{h\to 0} \frac{f(a+h)-f(a)}{h}\]

The definition above gives a function that maps input \(a\) to \(f'(a)\).
Simply replace "\(a\)" with the conventional notation for an input, i.e. "\(x\)", we have \[f'(x) = \lim_{h\to 0} \frac{f(x+h)-f(x)}{h}\] \(f'\) can be regarded as a new function, called derivative of \(f\).
Given an input \(x\), \(f'(x)\) is equal to the slope of the tangent line of \(f\) at the point (\(x,f(x)\)).

Example 1. If \(f(x)=x^2\), find \(f'\).
Sol: \[f'(x) = \lim_{h\to 0} \frac{f(x+h)-f(x)}{h} = \lim_{h\to 0} \frac{(x+h)^2-x^2}{h} = \lim_{h\to 0} \frac{2xh+h^2}{h} = \lim_{h\to 0} (2x+h) = 2x \]

Example 2. If \(f(x)=\sqrt{x}\), find \(f'\) and its domain.
Sol: \[\begin{aligned} f'(x)&=\lim_{h\to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}\\ &=\lim_{h\to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h} \frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}}\\ &=\lim_{h\to 0}\frac{(x+h)-x}{h(\sqrt{x+h}+\sqrt{x})}\\ &=\lim_{h\to 0}\frac{1}{\sqrt{x+h}+\sqrt{x}}\\ &=\lim_{h\to 0}\frac{1}{\sqrt{x}+\sqrt{x}} = \frac{1}{2\sqrt{x}} \end{aligned}\] The domain of \(f'(x)=\frac{1}{2\sqrt{x}}\) is \(x>0\). The domain of \(f(x)=\sqrt{x}\) is \(x\geq 0\).

Sketch \(f'\) Given Graph of \(f\)

Geometric interpretation: slope of \(f\) = derivative of \(f\)

How to tell \(f'(x)\) from the graph of \(f\): draw the tangent line of \(f\) at \((x,f(x))\), the slope of this tangent line is the value of \(f'(x)\)

Tricks:

Check where does \(f\) have a horizontal tangent line. If \(f\) has a horizontal tangent at \(x=a\), then \(f'(a)=0\).
Find the intervals on which \(f\) is increasing(going up), then \(f'>0\) over those intervals.
Find the intervals on which \(f\) is decreasing(going down), then \(f'<0\) over those intervals.

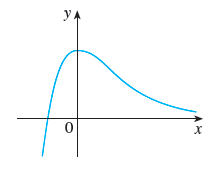
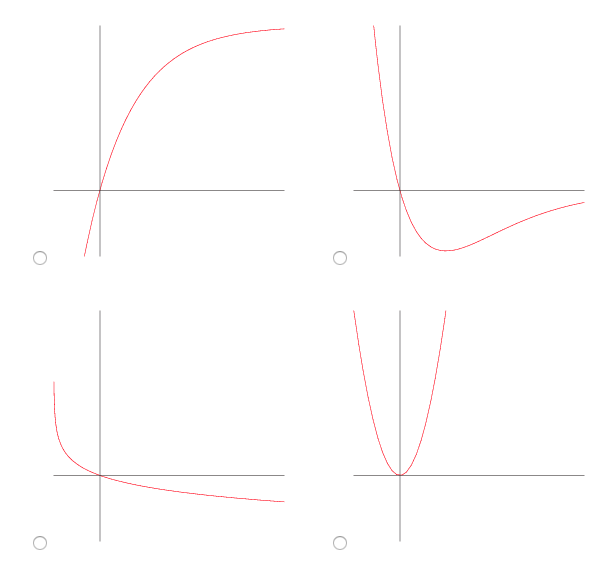
Example. If the graph of \(f\) is given below(blue curve), which is the graph of \(f'\)? Choose from the four red curves below.

Sol:

Note that the tangent line at \(x=0\) seems to be horizontal, so \(f'(0)\) is roughly \(0\).
\(f\) is increasing when \(x<0\), so \(f'(x)>0\) when \(x<0\).
\(f\) is decreasing when \(x>0\), so \(f'(x)<0\) when \(x>0\).
We see that as \(x\to\infty\), the slope of \(f(x)\) seems to approach \(0\). So we deduce that \(f'(x)\to 0\) as \(x\to\infty\).

The only graph that matches those observations is the top-right one.

Differentiability

Definition. We say \(f\) is differentiable at \(a\) if \(f'(a)\) exists. If it differentiable on \((a,b)\) if \(f'(x)\) exists for any \(x\) in \((a,b)\).

Tell differentiability from the graph of \(f\)

Three cases where \(f\) is not differentiable at \(x=a\):

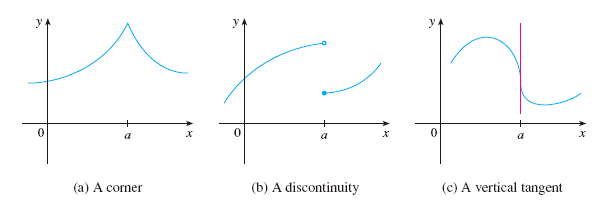
Theorem. If \(f\) is discontinuous at \(a\), then \(f\) is not differentiable at \(a\), i.e., \(f'(a)\) does not exist.

Higher Derivatives

\(f''(x)\) denotes the derivative of \(f'(x)\). \(f''\) is called the second derivative of \(f\).
\(f'''(x)\) denotes the derivative of \(f''(x)\). \(f'''\) is called the third derivative of \(f\).
In general, \(f^{(k)}\) denotes the \(k\)th derivative of \(f\).

Example. Velocity is the (first) derivative of the position function. Acceleration is the second derivative of the position function.

Another Notation

If \(y=f(x)\), then \(\frac{dy}{dx}=y'=f'(x)\) all denote derivative of \(f\).
\(\frac{d^2y}{dx^2}\) denotes \(f''\), the second derivative of \(f\).