

Remark. IVT does not invovle any derivative!
Let \(f\) be a function that satisfies the following three hypotheses:
Then there is a number \(c\) in \((a,b)\) such that \(f'(c)=0\).
Four functions that satisfy the assumptions in Rolles' Theorem:
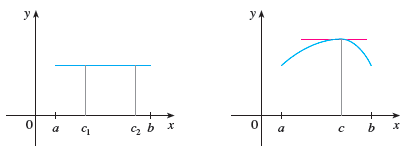
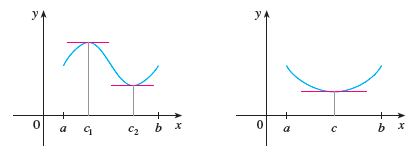
Example. Check if the assumptions in Rolles theorem are satisfied in the following cases.
(1). \(f(x)= \dfrac{1}{(x-1)^2}\) on \([0,2] \quad \)
(2). \(f(x)=|x|\) on \([-1,1]\quad\)
(3). \(f(x)=\sin x\) on \([0,\pi]\)
Example. Prove that the equation \(x^3+x-1=0\) has exactly one real root.


Example 1.
Find all numbers \(c\) that satisfy the conclusion of MVT for \(f(x)=3x^2-x+2\) on \([0,3]\).
Sol:
\[f'(c)=\dfrac{f(3)-f(0)}{3-0}\text{ for some } c\in (0,3)\]
That is,
\[6c-1=\dfrac{26-2}{3}=8\]
So \(c=\dfrac{3}{2}\) and \(c\) is indeed in \((0,3)\).
Example 2.
Find all numbers \(c\) that satisfy the conclusion of MVT for \(f(x)=x^3-x\) on \([0,2]\).
Sol:
\[f'(c)=\dfrac{f(2)-f(0)}{2-0}\text{ for some } c\in (0,2)\]
That is,
\[3c^2-1=\dfrac{6-0}{2}=3\]
So \(c^2=\dfrac{4}{3}\), \(c=\pm \sqrt{\dfrac{4}{3}}\). Recall that \(c\) should be in \((0,2)\), so \(c=\sqrt{\dfrac{4}{3}}\).
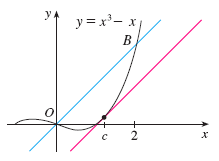
Example 3.
