Suppose \(f(x)\) is a function with domain \([a,b]\) and range \([p,q]\). The domain and range after transformation are shown below.
| transformation | domain | range | action |
|---|---|---|---|
| \(f(x)\) | \([a,b]\) | \([p,q]\) | debut |
| \(f(x)+s\) | \([a,b]\) | \([p+s,q+s]\) | vertical shift by \(s\) |
| \(f(x+s)\) | \([a-s,b-s]\) | \([p,q]\) | horizontal shift by \(-s\) |
| \(s f(x)\) | \([a,b]\) | \([sp,sq]\) | vertical scaling by \(s\) |
| \(f(sx)\) | \([\frac{a}{s},\frac{b}{s}]\) | \([p,q]\) | horizontal scaling by \(\frac{1}{s}\) |
| \(-f(x)\) | \([a,b]\) | \([-q,-p]\) | reflection about \(x\)-axis |
| \(f(-x)\) | \([-b,-a]\) | \([p,q]\) | reflection about \(y\)-axis |
Trick: You can actually tell what the transformation does to the graph of f(x)
from the change in the domain or range, e.g., a stretch, shift, reflection, etc.Definition. the composite function \(f\circ g\) is defined by \((f\circ g)(x) = f( g(x) )\). Namely, first apply \(g\) to \(x\), then apply \(f\) to the result.
The domain of \(f\circ g\) is the set of all \(x\) such that both \(g(x)\) and \(f(g(x))\) are well-defined.
Example. \(f(x)=\sqrt{x}\), \(g(x)=\sqrt{2-x}\).
Find the domain and expression of \(g\circ f\).
Solution:
We know that domain of \(f\) is \([0,\infty)\) and
domain of \(g\) is \((-\infty,2]\).
\((g\circ f)(x) = g\left(f(x)\right)\).
For \(g\left(f(x)\right)\) to make sense, we require:
\(f(x)\in (-\infty,2]\) and \(x\in [0,\infty)\), which implies,
\(x\in [0,4]\) .
Thus we conclude that \([0,4]\) is the domain of
\(g\circ f=g(f(x))=\sqrt{2-\sqrt{x}}\).
Example. \(F(x)=\sqrt{3+x^2}\). find \(f,g\) such that \(F=f\circ g\).
Solution:
Given an input, \(F\) does this:
You can check that \(F=f\circ g\).
\(f(x)=b^x\) is an exponential function because the variable, \(x\) is the exponent. The base \(b\) is a positive constant.
If \(b\neq 1\), domain: \(\mathbb{R}=(-\infty,\infty)\); range: \((0,\infty)\).
Examples. If \(n\) is a positive integer, \[f(n)=b^n=b \cdots b \quad (n \text{ factors}). \] Examples. \(f(0)=b^0=1\) and \[f(-x)=b^{-x}=\frac{1}{b^x}.\]
In addition to the renowned superstar number \(\pi\approx 3.14159\dots\), there is another number that is special enough to be endowed with its own symbol. That number is \[e\approx 2.71828\dots\]
The notation \(e\) was chosen by Euler (a famous Swiss mathematcian) and
the number is often called Euler's number.
We will see why the number \(e\) is singled out later when we learn derivatives of functions.
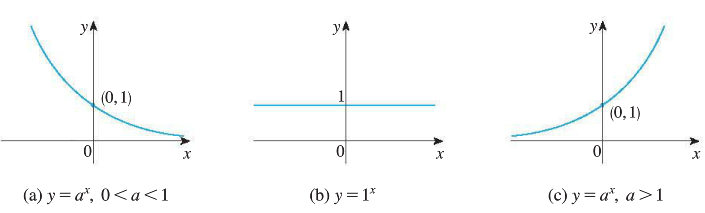
Graphs of \(f(x)=a^x\) for different values of \(a\):

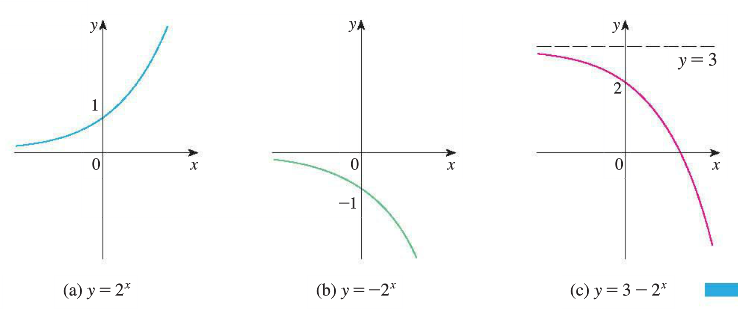
Example. Sketch the graph of the function \(y=3-2^x\) and determine its domain and range.
Domain: \(\mathbb{R}\); range: \((-\infty,3)\)
Ex. Find the domain of each function.
\((a).\; f(x)=\frac{1+e^x}{1-e^{x}}\quad
(b).\; g(t)=\sqrt{10^t-100}\quad
(c).\; f(t)= \frac{\cos t}{e^t}\)
Answer: (a). \(x\neq 0\); (b). \(t\geq 2\); (c). \((-\infty,\infty)\)
Law of Exponents: \[b^{x+y}=b^x b^y,\quad (b^x)^y=b^{xy},\quad (ab)^x=a^x b^x\]
Ex. Simplify the following expressions: \[(a)\; 8^{4/3}\quad (b)\; \frac{1}{\sqrt[3]{x^4}}\quad (c).\; x(3x^2)^3 \quad (d).\; \frac{x^{3}x^{2k}}{x^{k+2}} \] Answer: \((a). 2^4=16 \quad (b). x^{-4/3}\quad (c). 27x^{7}\quad (d). x^{k+1}\)
Example. Assume the volume of ice \(F\) on an unknown planet decays with respect to time \(t\)(year) in the following pattern:
every 5 years, the volume shrinks by half.
If the volume today (year \(0\)) is \(1836\) degrees. Find the volume \(F\) at year \(t\).
Solution:
\[
\begin{aligned}
F(0) &=1836 \\
F(5) &= \frac{1}{2}(1836) \\
F(10) &= \frac{1}{2}\frac{1}{2}(1836)=\frac{1}{2^2}(1836) \\
F(15) &= \frac{1}{2}\frac{1}{2^2}(1836)=\frac{1}{2^3}(1836)
\end{aligned}
\]
We deduce that
\[F(t) = \frac{1}{2^{t/5}}(1836)=1836 (2^{-1/5})^t.\]