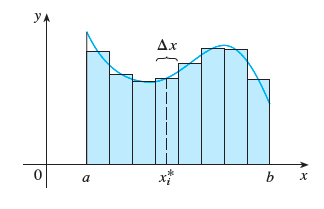
Definition of (signed) area. Let \(f\) be continuous on \([a,b]\). Divide \([a,b]\) into \(n\) subintervals of equal width \(\Delta x=\frac{b-a}{n}\). Denote by \(x_0=a, \, x_1,\, x_2,\, \dots,\, x_n=b\) the endpoints of subintervals. Let \(x_i^*\) be the sample point in the \(i\)th subinterval \([x_{i-1},x_i]\), where \(i=1,\dots,n\). Then the area under the graph of \(f\) is given by \[A=\lim_{n\to \infty}[f(x_1^*)\Delta x+ \dots + f(x_n^*)\Delta x]=\lim_{n\to\infty}\sum_{i=1}^n f(x_i^*)\Delta x\]
Signed area: The "area" can be negative if \(f\) is negative. For example, if \(f=-5\), \([a,b]=[0,2]\), then \(A=(-5)\times 2=-10.\)
Definition of a Definite Integral Under the same assumption as in the definition of area, the definite integral of \(f\) from \(a\) to \(b\) is \[\int_a^b f(x) dx = \lim_{n\to\infty}\sum_{i=1}^n f(x_i^*)\Delta x\]
Explanation of Notation: "\(\int\)" is a (vertically) strechted version of "\(S\)" (which indicates "Sum" or "Sigma"). "\(dx\)" is a variation of "\(\Delta x\)" ("Delta \(x\)").
Dummy variable. The \(x\) in \(\int_a^b f(x) dx\) is a "dummy variable", it can be replaced by any other notations. \(\int_a^b f(t) dt\), \(\int_a^b f(W) dW\)... all mean the same thing.
Riemann Sum. The sum \(\sum_{i=1}^n f(x_i^*)\Delta x\) is called a Riemann sum.
Sample Points. You are free to choose the sample point \(x_i^*\) in \([x_{i-1},x_i]\). For example, you can choose samples points to be left endpoints (\(x_i^*=x_{i-1}\)), right endpoint (\(x_i^*=x_{i-1}\)), midpoints (\(x_i^*=\frac{x_{i-1}+x_i}{2}\)), etc.

Example 1.
Find the integral \(\int_{1}^3 f(x)\;dx\),
where \[f(x)=\begin{cases} 2 & \text{if } x<2 \\ x & \text{if } x>2\end{cases}.\]
Sol:
The area under the graph of \(f\) over the interval \([1,3]\) is \(4.5\). So \(\int_{1}^3 f(x)\;dx=4.5\).
Example 2.
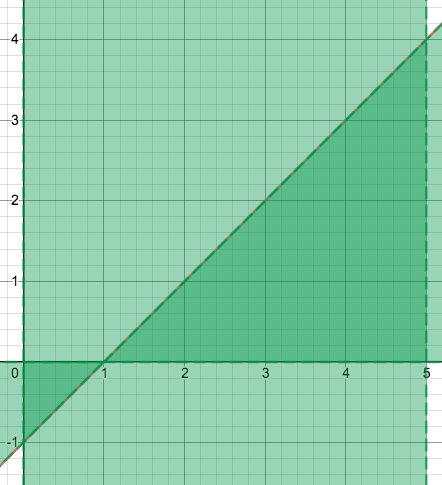
Find the integral \(\int_{0}^5 (x-1) \;dx\).
Sol: \(f(x)=x-1\) and the interval is \([0,5]\).
The region of interest is enclosed by the curve of \(f(x)=x-1\), the \(x\)-axis, the vertical lines \(x=0\) and \(x=5\). The region is composed of two triangles, illustrated in the figure below (see the darker green area).
The area of the triagnle below \(x\)-axis is \(\frac{1}{2}\) and the area of the triangle above \(x\)-axis is \(\frac{4\cdot 4}{2}=8\).
\[\int_{0}^5 (x-1) \;dx=\int_0^1 (x-1)\; dx+\int_1^5 (x-1)\; dx=-\frac{1}{2}+8=7.5,\]
where the \(-\frac{1}{2}\) is the signed area of the triangle below \(x\)-axis.
To simplify the calculation of the integral we often take the sample points to be right endpoints. Then \(x_i^*=x_i\) and the definition of an integral simplifies as follows. \[\int_a^b f(x) dx = \lim_{n\to\infty}\sum_{i=1}^n f(x_i) \Delta x= \lim_{n\to\infty}\sum_{i=1}^n f(a+i\Delta x) \Delta x\] where \(x_i=a+i\Delta x\), \(\Delta x=\frac{b-a}{n}\).
Ex. Express \(\int_{1}^5 \sqrt{1+x}\; dx\) as a limit of Riemann sums. Do not evaluate the limit.
Key: \(\lim_{n\to\infty}\sum_{i=1}^n \dfrac{4}{n}\sqrt{1+\frac{4i}{n}} \)
Ex. Express \(\lim_{n\to\infty}\sum_{i=1}^n x_i^* \cos(x_i^*)\Delta x, \; [0,3]\) as a definite integral on the given interval.
Key: \(\int_0^3 x\cos x dx\)
\[\int_a^b f(x) dx + \int_b^c f(x) dx = \int_a^c f(x) dx\]
Example.
If \(\int_0^2 f(x)dx = 5\) and \(\int_0^3 f(x)=1\),
find \(\int_2^3f(x)dx.\)
Sol:
\[\int_0^2 f(x)dx+\int_2^3 f(x)dx=\int_0^3 f(x)dx\]
So \[5+\int_2^3 f(x)dx=1.\]
Then \(\int_2^3 f(x)dx=-4.\)