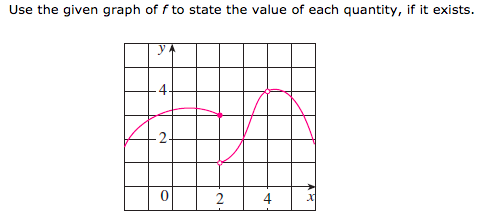
\((a). \lim_{x\to 2^-} f(x) \quad (b). \lim_{x\to 2^+} f(x)\quad (c). f(2)\quad (d). \lim_{x\to 2} f(x)\quad (e). \lim_{x\to 4} f(x) \)
Suppose \(f(x)\) is defined when \(x\) is near the number \(a\), then \[\lim_{x\to a} f(x) = L\] if we can make values of \(f(x)\) arbitrarily close to \(L\) by restricting \(x\) to be sufficiently close \(a\) (on either side of \(a\)) but not equal to \(a\).
Consider the Heaviside function \[H(t)=\begin{cases} 0 \quad\text{if}\quad t<0, \\ 1\quad\text{if} \quad t\geq 0. \end{cases}\] \[\lim_{t\to 0^-}H(t)=0\quad\text{and}\quad \lim_{t\to 0^+}H(t)=1\] Here \(t\to 0^-\) means \(t\) approaches \(0\) from the left (\(t<0\)), and \(t\to 0^+\) from the right of \(0\) (\(t>0\)).

\((a). \lim_{x\to 2^-} f(x) \quad
(b). \lim_{x\to 2^+} f(x)\quad
(c). f(2)\quad
(d). \lim_{x\to 2} f(x)\quad
(e). \lim_{x\to 4} f(x)
\)
Limit and one-sided limits: \[\lim_{x\to a} f(x)=L\quad\text{if and only if}\quad \lim_{x\to a^-}f(x)=L\text{ and } \lim_{x\to a^+}f(x)=L\]
\(\lim_{x\to a}f(x)=\infty\) means that the values of \(f(x)\) can be made arbitrarily large by taking \(x\) sufficiently close to \(a\), but not equal to \(a\). ( \(f(x)\) "blows up" when \(x\) approaches \(a\) )
Since \(\infty\) is not a number, \(\lim_{x\to a}f(x)=\infty\) implies that the limit doest not exist when \(x\) tends to \(a\).
Similarly, \(\lim_{x\to a}f(x)=\infty\) means that \(f(x)\) can be arbitrarily large negative as \(x\) approaches \(a\).
Example. \(\lim_{x\to 0}\frac{1}{x^2}=\infty\) and \(\lim_{x\to 0}\frac{-1}{x^2}=-\infty\)
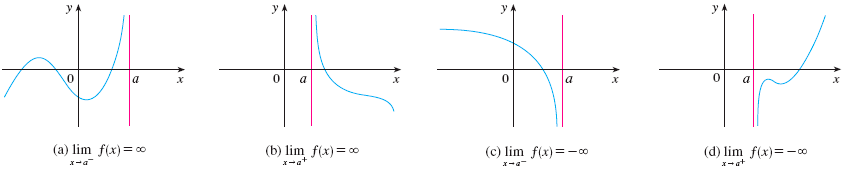
One-sided infinite limits can be defined similarly (see graphs below).
If \(f(x)\) tends to \(\infty\) or \(-\infty\) as \(x\) approaches \(a\) (either one-sided or two-sided), the vertical line \(x=a\) is called a vertical asymptote of \(y=f(x)\).
Ex. Find the limits.
(a). \(\lim_{x\to 4^-} \frac{5-x}{x-4}\)
(b). \(\lim_{x\to 1^+}\ln(x^2-1)\)
(c). \(\lim_{x\to (\frac{\pi}{2})^-} \tan x\)
(d). \(\lim_{x\to (\frac{\pi}{2})^+} \tan x\)
Answer: (a).\(-\infty\) (b). \(-\infty\)
(c).\(\infty\) (d).\(-\infty\)
Assume \(\lim_{x\to a} f(x)\) exists. Then
Ex. (a). \(\lim_{x\to 1} \sqrt[3]{x^2-9}\)
(b). \(\lim_{x\to -1} 3x-5x^2+1\)
Answer: (a). -2 (b). -7
Assume that the limits \(\lim_{x\to a} f(x)\) and \(\lim_{x\to a} g(x)\) exist. Then
What if \(\lim_{x\to a} g(x) =0\) ? See below.
In this case, it is very likely that the expression can be simlified by canceling out common factors from the top and the bottom.
Example 1. \(\lim_{x\to 1} \frac{1-x^2}{x-1}\)
Solution: \(\lim_{x\to 1} x-1 = 0\) so we cannot apply the law above.
Instead, we first simplify the expression:
\[\frac{1-x^2}{x-1} = \frac{(1+x)(1-x)}{x-1} = -(1+x)\]
Now it follows that \(\lim_{x\to 1} \frac{1-x^2}{x-1} = \lim_{x\to 1} -(1+x)=-2\).
Example 2. \(\lim_{x\to 0} \frac{(1-h)^2-1}{h}\)
Solution: Since \((1-h)^2-1=-2h+h^2\),
we have \[\lim_{x\to 0} \frac{(1-h)^2-1}{h} = \lim_{x\to 0} \frac{-2h+h^2}{h}=\lim_{x\to 0} -2+h = -2\]
Example 3. \(\lim_{t\to 9} \frac{9-t}{3-\sqrt{t}}\)
Solution:
\[\lim_{t\to 9} \frac{9-t}{3-\sqrt{t}}=\lim_{t\to 9} \frac{9-t}{3-\sqrt{t}} \frac{3+\sqrt{t}}{3+\sqrt{t}}=\lim_{t\to 9} \frac{(9-t)(3+\sqrt{t})}{9-t}=\lim_{t\to 9}3+\sqrt{t}=6\]