Definition.
A function \(f\) is continuous at \(a\) if
\(\lim_{x\to a}f(x)=f(a)\).
We say \(f\) is discontinuous at \(a\) if \(f\) is not continuous at \(a\).
Three things to check to determine the continuity of \(f\) at \(a\):
1. \(f(a)\) is defined (that is, \(a\) is in the domain of \(f\))
2. \(\lim\limits_{x\to a}f(x)\) exists
3. \(\lim\limits_{x\to a}f(x)=f(a)\)
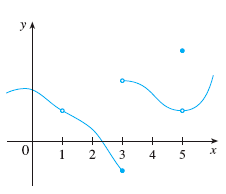
Example. The graph of \(f\) is shown below. Discuss the continuity of \(f\) at \(x=1\), \(x=3\), \(x=5\).

Solution: \(f\) is discontinuous at \(x=1\) because \(f(1)\) is not defined.
\(f\) is discontinuous at \(x=3\) because \(\lim\limits_{x\to 3} f(x)\) does not exist (two sided limits are not equal).
\(f\) is discontinuous at \(x=5\) because
\(\lim\limits_{x\to 5} f(x)\neq f(5)\).
Example. Is \(f(x)=\tan x\) continuous at \(x=0\) ? what about at \(x=\frac{\pi}{2}\) ?
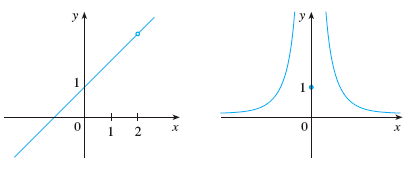
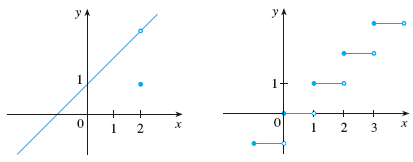
Types of discontinuities:
(1).top left: \(f(2)\) undefined, removable discontinuity
(2).top right: \(\lim\limits_{x\to 0} f(x)=\infty\), infinite discontinuity
(3).bottom left: \(\lim\limits_{x\to 2} f(x)\neq f(2)\), removable discontinuity (we can redefine \(f(2)\) so that \(f\) becomes continuous after the redefinition)
(4).bottom right: jump discontinuities at \(x=0, 1, 2, 3\)
Ex. Where are each of the following functions discontinuous?
(a). \(f(x)=\frac{x^2+2x-3}{x-1}\)
(b). \(f(x)=\begin{cases} \frac{1}{x^2} &\text{if}\; x\neq 0\\ 1 &\text{if}\; x=0 \end{cases}\)
Hint: (a). just find points that are not in the domain of \(f\);
(b). what is \(\lim\limits_{x\to 0} f(x)\)
Besides, you can also see from their graphs above (the ones at the top)
Definition. A function \(f\) is continuous on an interval if it is continuous at every point in the interval. (continuity at endpoint is interpreted as one-sided continuity)
Ex. Show that \(f(x)=\sqrt{1-x^2}\) is continuous over \([-1,1]\).
Answer: see textbok Example 4 in Section 2.5
"Theorem". All essential functions in math 111 as well as their compositions are continuous at every point in their domains.
Ex. \(f(x)=\frac{2}{x-1}\), \(g(x)=\frac{x^2}{x-1}\).
Find where each of the funcitons below are continuous.
(a). \(f-g\); (b). \(fg\) (c). \(f/g\)
Hint: According to "Theorem", it suffices to find their domains
Answer: (a). \(x\neq 1\);
(b). \(x\neq 1\);
(c). \(x\neq 1\) and \(x\neq 0\) (that is \((-\infty,0)\cup (0,1)\cup (1,\infty)\))
Caveat: domain of \(f\pm g\), \(fg\), \(f/g\) has to be contained in domain of \(f\) and domain of \(g\).
Theorem. Suppose that \(f\) is continuous on the closed interval \([a,b]\). Let \(Q\) be any number between \(f(a)\) and \(f(b)\), where \(f(a)\neq f(b)\). Then there exists a number \(c\) in \((a,b)\) such that \(f(c)=Q\).
Corollory.
Let \(f\) be continuous over \([a,b]\).
If \(f(a)\cdot f(b)<0\), then there must be a number \(c\) between \(a\) and \(b\) such that \(f(c)=0\).
(think of the graph of \(f\): it has to cut \(x\)-axis at some point)
Application.(estimating root of an equation) Show that there is a root of \(x^5-10x+1=0\) between \(1\) and \(2\).