
We write
\[\lim\limits_{x\to\infty}f(x)=L\]
if \(f(x)\) gets arbitrarily close to \(L\)
as \(x\) approaches \(\infty\).
The line \(y=L\) is called a horizontal asymptote of the graph of function \(f\).
(Similarly, \(\lim\limits_{x\to-\infty}f(x)=L\) is the limit when \(x\) approaches \(-\infty\))

Find \(\lim\limits_{x\to\infty} f(x)\) or \(\lim\limits_{x\to-\infty} f(x)\) if the graph of \(f\) is as below:
(a).
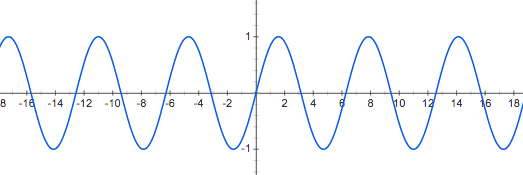
(b).

(c).
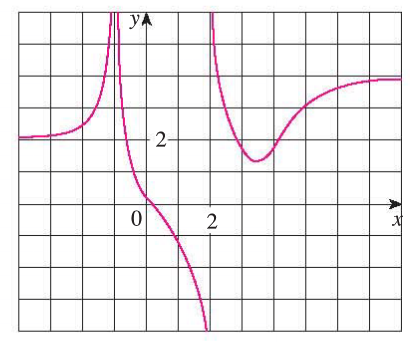
Answer:
(a). both limits DNE;
(b). \(\lim\limits_{x\to \infty}f(x)=\pi/2\) and
\(\lim\limits_{x\to -\infty}f(x)=-\pi/2\);
(c). \(\lim\limits_{x\to \infty}f(x)=4\) and
\(\lim\limits_{x\to -\infty}f(x)=2\);
Example 1. \(\lim\limits_{x\to\infty} \frac{1}{x} = 0\) and \(\lim\limits_{x\to-\infty} \frac{1}{x} = 0\)
Example 2. \(\lim\limits_{x\to\infty} \frac{x}{x^2-x} = \lim\limits_{x\to\infty} \frac{x}{x^2}=0\)
Example 3. \(\lim\limits_{x\to\infty} \frac{2x^2}{3x^2-x} = \lim\limits_{x\to\infty} \frac{2x^2}{3x^2}=\frac{2}{3}\)
Example 4. \(\lim\limits_{x\to\infty} \frac{2x^2+x-5}{3x^2+4x+1} = \lim\limits_{x\to\infty} \frac{2x^2}{3x^2}=\frac{2}{3}\)
Example 5. \(\lim\limits_{x\to\infty} \frac{\sqrt{2x^2+x-5}}{3x^2+4x+1} = \lim\limits_{x\to\infty} \frac{\sqrt{2x^2}}{3x^2}=\lim\limits_{x\to\infty}\frac{\sqrt{2}}{3x}=0\)
Example 6. \(\lim\limits_{x\to\infty} \sqrt{x^2+1} -x = \lim\limits_{x\to\infty} x-x=0\)
Example 7. \(\lim\limits_{x\to\infty} (x^2-x) = \lim\limits_{x\to\infty} x^2 = \infty\) (it's wrong to write it as \(\lim\limits_{x\to\infty} x^2-\lim\limits_{x\to\infty} x\))
Example 8. \(\lim\limits_{x\to-\infty} e^{1/x} = \lim\limits_{t\to0^-} e^t = e^0 = 1\)
Example 9. \(\lim\limits_{x\to-\infty} \sin x = DNE\)
Example 10. \(\lim\limits_{x\to\infty} \arctan x = \pi/2\) and \(\lim\limits_{x\to-\infty} \arctan x = -\pi/2\) (graph of \(y=\arctan x\) is (b) above)
Example 11. \(\lim\limits_{x\to-\infty} (e^x+9) = 9\)
Trick used in Examples 2 to 7: for polynomials, just ignore lower order terms
when finding limit as x tends to infinity (either positive or negative).
That is, it suffices to compute with the highest order term only.