index

Welcome to choose this class!
For any questions regarding enrollment, please contact Prof. Ettinger: bree.d.ettinger@emory.edu.
There is no class meeting on Monday April 12th due the rest day of the week.

Lecture Instructor	Dr. Le Chen
Lab Instructor	Xingjian Li
Email	le.chen@emory.edu, xingjian.li@emory.edu (please include "Math 221" in the subject field of your email)
Synchronous Session	Monday 11:20AM -- 12:35PM
Office hours	Monday and Wednesday 1:00pm -- 2:00pm, or by appointments
Lab Sessions	Friday, 9:40AM -- 10:30AM for Math221-1 and 11:20AM -- 12:10PM for Math221-2
Zoom link for class	https://emory.zoom.us/j/94863155226?pwd=NjducFE0b3hFQ2V0MVYxVXptS2Rxdz09

The password for both Zoom links are on Canvas page.
The Zoom link for class is for all synchronous/lab sessions, office hours, and independent appointments.
When you send us emails, please do include the keyword Math221 in the subject field of your email to ensure a timely response.

Course description

_{(Image from Wikipedia)}

Linear algebra is a branch of mathematics concerning linear equations such as \(a_1 x_1 + \cdots + a_n x_n = b\), linear maps such as \((x_1,\cdots,x_n) \mapsto a_1x_1 + \cdots + a_n x_n\), and their representations in vector spaces and through matrices. Linear algebra is central to almost all areas of mathematics. It is also used in most sciences and engineering areas.

This course begins with the definition of a matrix and some fundamental operations that can be performed on matrices, such as adding or multiplying two matrices together. Vector spaces are also introduced. A connection is then formed by modeling vector spaces using matrices. Advanced topics involving matrices, such as diagonalization and quadratic forms, eigenvalues and eigenvectors, orthogonalization, and the Gram-Schmidt process are examined. At the end of the class, you will understand how google ranks web pages.

Textbook

We will use the following online book which is free to download:

	Original Textbook	Customized Textbook
Bookcover
For a hard copy	https://lyryx.com/linear-algebra-applications/
Download	Nicholson-OpenLAWA-2019A.pdf	Adapted_Textbook_Math221-1_2_Emory-Spring2021.pdf
Edition	2019 Revision A	Check the date on the front page in red

We will update the adapted textbook throughout the semester; please double check the date on the front page in the red color for versions.

The book consists of eleven chapters, we will cover most parts of the first eight chapters:

Chapter 1. Systems of Linear Equations.
Chapter 2. Matrix Algebra
Chapter 3. Determinants and Diagonalization
Chapter 4. Vector Geometry
Chapter 5. Vector Space \(\mathbb{R}^n\)
Chapter 6. Vector Spaces
Chapter 7. Linear Transformations
Chapter 8. Orthogonality
~~Chapter 9. Change of Basis~~
~~Chapter 10. Inner Product Spaces~~
~~Chapter 11. Canonical Forms~~

Six hours of AP BC credit, or
Math 12 or 112Z

By the end of this course, students will be able to

Solve system of linear equations, perform matrix operations, find the inverse of a matrix, check vectors for linear independence.
List the vector space properties for \(\mathbb{R}^n\), give examples of subspaces, find bases for subspaces, find its dimension, find orthogonal bases for subspaces, identify linear transformations.
Find eigenvalues and eigenvectors, determinants, characteristic polynomial, perform diagonalization of a matrix.
Give examples of vector spaces, check for linear independence, find bases, dimension, identify linear transformations and find matrix representation for linear transformations.

In order to successfully master the material and complete the course, you are expected to

Read the textbook and watch video posted on Canvas.
Take the advantage of the lab session and office hours, which give you additional chance to interact lively with the instructors.
Since problems solved or question/answers in the office hour will be beneficial to other students, be default the office hours will be recorded automatically.
In case you do not want put the office hours on Canvas, please let me know.
Attend weekly Zoom class meeting and weekly lab session, and watch video recordings for the asynchronous materials.
Participate actively in group activities during Zoom meetings.
Complete and submit weekly homework through Gradescope.
Read solutions and any feedback you receive for each problem set.
Complete three midterm tests and one final exam.
Use appropriate etiquette and treat other students with respect in all discussions.
Do not hesitate to ask for help whenever needed.

Note: The syllabus was created in Nov. 2020, and it is subject to changes during the semester.

There will be roughly thirteen weekly homework assignments scheduled as follows:

Releasing	Due at
Monday 6:00pm EST	Friday, 6pm EST

No late homework will be accepted.
The homework consists two phases:
- In Phase I, you need to complete questions on canvas.
  - You will have two attempts, and the best score will be recorded.
  - There is no time limit on Phase I. But be mindful that by the deadline line, the unfinished quiz will be automatically submitted by the system.
- In Phase II, you need to write details of your solutions and upload them to gradescope.
The lowest grade will be dropped, that is, the final score for the homework will be averaged over the rest HWs.
- Note that the drop policy is not a bonus. It aims at accounting for all circumstances
  such as sickness, injuries, family emergencies, religion holidays, etc.

There will be three midterm tests starting from the following three Fridays.

	Releasing at	Due at	Coverage
Test I	02/12/2021, 6pm EST	02/13/2021, 6pm EST	Chapters 1 & 2
Test II	03/05/2021, 6pm EST	03/06/2021, 6pm EST	Chapters 3 & 4
Test III	04/02/2021, 6pm EST	04/03/2021, 6pm EST	Chapters 5 & 6
Final Exam	05/06/2021, 8am EST	05/07/2021, 8am EST	Chapters 1 -- 8, comprehensive

Please note down the above three dates. The setup has taken into account of different time zones.
Hence, no late exam and further extension will be given.
The test consists two phases:
- In Phase I, you need to complete questions on canvas.
- In Phase II, you will have 24 hours to complete take-home problems and upload your solutions to Gradescope.
- Unlike the homework, the phase I of tests will have a time limit of 60 minutes:
  - Once it is started, please do complete it in 60 minutes.
  - Make sure your start before 5pm of the second day.
  - At 6pm your ongoing quiz will be automatically submitted by the system.
- You will have two attempts and the best score will be counted as your test score.

Test one covers Sections 1.1--1.3 and 2.1--2.7.
Phase-I will consist of 5 choice-problems on Canvas Quiz: Two from Chapter 1 and three from Chapter 2. There are \(5\times 12=60\) points.
Phase-II consists of three problems: all from Chapter 2. There are \(10+20+10=40\) points.

Here are a list of due dates for 12 homeworks and three tests (the Phase II part).

	Monday		Friday			Saturday
Week 1	01/25	HW01 releases at 6pm EST	01/29	HW01 due at 6pm EST
Week 2	02/01	HW02 releases at 6pm EST	02/05	HW02 due at 6pm EST
Week 3	02/08	HW03 releases at 6pm EST	02/12	HW03 due at 6pm EST	Test I releases at 6pm EST	02/13	Test I due at 6pm
Week 4	02/15	HW04 releases at 6pm EST	02/19	HW04 due at 6pm EST
Week 5	02/22	HW05 releases at 6pm EST	02/26	HW05 due at 6pm EST
Week 6	03/01	HW06 releases at 6pm EST	03/05	HW06 due at 6pm EST	Test II releases at 6pm EST	03/06	Test II due at 6pm
Week 7	03/08	HW07 releases at 6pm EST	03/12	HW07 due at 6pm EST
Week 8	03/15		03/19				(no assignment week)
Week 9	03/22	HW08 releases at 6pm EST	03/26	HW08 due at 6pm EST
Week 10	03/29	HW09 releases at 6pm EST	04/02	HW09 due at 6pm EST	Test III releases at 6pm EST	04/03	Test III due at 6pm
Week 11	04/05	HW10 releases at 6pm EST	04/09	HW10 due at 6pm EST
Week 12	04/12	HW11 releases at 6pm EST	04/16	HW11 due at 6pm EST
Week 13	04/19	HW12 releases at 6pm EST	04/23	HW12 due at 6pm EST
Week 14	04/26	Review Session

Final exam will be cumulative, which covers Chapters 1-8.
It will be in a similar form as the midterm tests, namely, you will have two phases.
Exam will be released on May 6th Thursday at 8am EST and be due on May 7th Friday at 8am EST.
You need to complete both Phases in 24 hours.
For Phase I, once you start, you will have only 150 minutes to complete.
There will be two attempts and the best one will be recorded.
There will be 15 problems and 5 points for each problem: \(5\times 15=75\) points.
There will be one bonus problem in Phase I. So do not be surprised to see 16 problems.
If you score 80 in Phase I, it will be counted as 75.
You will have two attempts and the highest attempt will be recorded.
Phase II consists of two randomized problems, 25 points in total.
At around 7:50am on May 6th EST, the phase II part will be sent out by email.
You need to upload your solutions to Gradescope by May 7th 8am EST.

The attendance will be collected during Zoom automatically.
Attendance will not directly counted into your final score.
But sufficient attendance will make your eligible for grade curving at the end of semester.

The final score will be determined as follows:
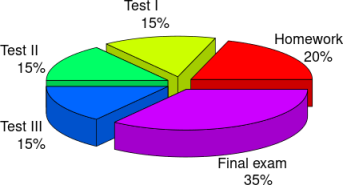
Based on the final score (plus potential bonus points), the final letter grade will be determined as follows:

Grade (+)		Grade		Grade (-)
		A	92%-100%	A-	90%-91.9%
B+	87%-89.9%	B	82%-86.9%	B-	80%-81.9%
C+	77%-87.9%	C	72%-76.9%	C-	70%-71.9%
D+	67%-67.9%	D	67%-67.9%	D-	60%-61.9%
		F	0%-59.9%

Since we will have scores in both Canvas and Gradescope, you are encouraged to can download this spread sheet to keep track of your progress.

Text and slides

You can download text for each chapter or section below.
Slides will be updated constantly throughout the semester and please check the time stamp on the front page.
The application parts of each chapter will be skipped due to lack of time. However, the materials are given for motivated students to study.

Chapter/Section	Textbook		Slides
Chapter 1. Systems of Linear Equations	original text	adapted text
Section 1-1. Solutions and Elementary Operations	original text	adapted text	presentation	handout
Section 1-2. Gaussian Elimination	original text	adapted text	presentation	handout
Section 1-3. Homogeneous Equations	original text	adapted text	presentation	handout
~~Section 1-4. An Application to Network Flow~~	original text
~~Section 1-5. An Application to Electrical Network~~	original text		presentation	handout
~~Section 1-6. An Application to Chemical Reactions~~	original text		presentation	handout
Section 1-S. Supplementary Exercises for Chapter 1	original text	adapted text
Chapter 2. Matrix Algebra	original text	adapted text
Section 2-1. Matrix Addition and Scalar Multiplication and Transportation	original text	adapted text	presentation	handout
Section 2-2. Matrix-Vector Multiplication	original text	adapted text	presentation	handout
Section 2-3. Matrix Multiplication	original text	adapted text	presentation	handout
Section 2-4. Matrix Inverses	original text	adapted text	presentation	handout
Section 2-5. Elementary Matrices	original text	adapted text	presentation	handout
Section 2-6. Linear Transformations	original text	adapted text	presentation	handout
Section 2-7. LU-Factorization	original text	adapted text	presentation	handout
~~Section 2-8. An Application to Input-Output Economic Model~~	original text
~~Section 2-9. An application to Markov Chains~~	original text		presentation	handout
Section 2-S. Supplementary Exercises for Chapter 2	original text	adapted text
Chapter 3. Determinants and Diagonalization	original text	adapted text
Section 3-1. The Cofactor Expansion	original text	adapted text	presentation	handout
Section 3-2. Determinants and Matrix Inverses	original text	adapted text	presentation	handout
Section 3-3. Diagonalization and Eigenvalues	original text	adapted text	presentation	handout
~~Section 3-4. An Application to Linear Recurrences~~	original text		presentation	handout
~~Section 3-5. An Application to Systems of Differential Euqations~~	original text
Section 3-6. Proof of the Cofactor Expansion Theorem	original text	adapted text
Section 3-S. Supplementary Exercises for Chapter 3	original text	adapted text
Chapter 4. Vector Geometry	original text	adapted text
Section 4-1. Vectors and Lines	original text	adapted text	presentation	handout
Section 4-2. Projections and Planes	original text	adapted text	presentation	handout
Section 4-3. More on the Cross Product	original text	adapted text	presentation	handout
Section 4-4. Linear Operators on R3	original text	adapted text	presentation	handout
~~Section 4-5. An Application to Computer Graphics~~	original text
Section 4-S. Supplementary Exercises for Chapter 4	original text	adapted text
Chapter 5. Vector Space Rn	original text	adapted text
Section 5-1. Subspaces and Spanning	original text	adapted text	presentation	handout
Section 5-2. Independent and Dimension	original text	adapted text	presentation	handout
Section 5-3. Orthogonality	original text	adapted text	presentation	handout
Section 5-4. Rank of a Matrix	original text	adapted text	presentation	handout
Section 5-5. Similarity and Diagonalization	original text	adapted text	presentation	handout
~~Section 5-6. Best Approximation and Least Squares~~	original text
~~Section 5-7. An Application to Correlation and Variance~~	original text	adapted text
Section 5-S. Supplementary Exercises for Chapter 5	original text	adapted text
Chapter 6. Vector Spaces	original text	adapted text
Section 6-1. Examples and Basic Properties	original text	adapted text	presentation	handout
Section 6-2. Subspaces and Spanning Sets	original text	adapted text	presentation	handout
Section 6-3. Linear Independence and Dimensions	original text	adapted text	presentation	handout
Section 6-4. Finite Dimensional Spaces	original text	adapted text	presentation	handout
~~Section 6-5. An Application to Polynomials~~	original text
~~Section 6-6. An Application to Differential Equations~~	original text
Section 6-S. Supplementary Exercises for Chapter 6	original text	adapted text
Chapter 7. Linear Transformations	original text	adapted text
Section 7-1. Examples and Elementary Properties	original text	adapted text	presentation	handout
Section 7-2. Kernel and Image of a Linear Transformation	original text	adapted text	presentation	handout
Section 7-3. Isomorphisms and Composition	original text	adapted text	presentation	handout
~~Section 7-4. A Theorem about Differential Equations~~	original text
~~Section 7-5. More on Linear Recurrences~~	original text
Chapter 8. Orthogonality	original text	adapted text
Section 8-1. Orthogonal Complements and Projections	original text	adapted text	presentation	handout
Section 8-2. Orthogonal Diagonalization	original text	adapted text	presentation	handout
Section 8-3. Positive Definite Matrices	original text	adapted text	presentation	handout
Section 8-4. QR-Factorization	original text	adapted text	presentation	handout
Section 8-5. Computing Eigenvalues	original text	adapted text	presentation	handout
Section 8-6. The Singular Value Decomposition	original text	adapted text	presentation	handout
~~Section 8-7. Complex Matrices~~	original text
~~Section 8-8. An Application to Linear Codes over Finite Fields~~	original text
~~Section 8-9. An Application to Quadratic Forms~~	original text
~~Section 8-10. An Application to Constrained Optimization~~	original text
~~Section 8-11. An Application to Statistical Principal Component Analysis~~	original text

Below is the tentative schedule that may change during the semester:

	Monday -- Friday	Coverage
Week 1	01/25 -- 01/29	1.1 -- 1.3
Week 2	02/01 -- 02/05	2.1 -- 2.4
Week 3	02/08 -- 02/12	2.5 -- 2.7 (Test I)
Week 4	02/15 -- 02/20	3.1 -- 3.2
Week 5	02/22 -- 02/27	3.3
Week 6	03/01 -- 03/05	4.1 -- 4.3 (Test II)
Week 7	03/08 -- 03/12	5.1 -- 5.2, 5.4
Week 8	03/15 -- 03/19	5.3 and 5.5 (no assignment week)
Week 9	03/22 -- 03/26	6.1 -- 6.2
Week 10	03/29 -- 04/02	6.3 -- 6.4 (Test III)
Week 11	04/05 -- 04/09	7.1, 8.1 -- 8.2
Week 12	04/12 -- 04/16	8.3 -- 8.4 (Rest day on Monday)
Week 13	04/19 -- 04/23	7.2 -- 7.3, 8.6
Week 14	04/26	Reviewing week

We will use Gradescope to handle submissions of homework, take-home tests and exams,
which allows us to provide fast and accurate feedback on your work.
As soon as grades are posted, you will be notified immediately so that you can log in and see your
grades and feedback.
Your Gradescope login is your university email, and your password can be changed there. The same
link can be used if you need to set your password for the first time.
- You should have received an email from Gradescope for the registration by 2021-01-23.
- If you do not receive this email, please use the Entry Code to register yourself: BPPGR4.
If you have any questions regarding Gradescope, please send your message to
- help@gradescope.com
Printer+scanner or tablet
- The easiest way to submit the homework/tests/exams is the following steps:
  1. print the given template;
  2. complete the problem sets;
  3. scan the resulting paper (make sure it is legible);
  4. upload the scanned file to gradescope.
- Alternatively, if you have a tablet that you can write on it, you may simply write on the
  template pdf file and upload the resulting file.
- Make sure that you make the correct association of your solutions to the problems.
- Double check your scan quality and make sure your solutions are legible.
The following short video (1 minutes 40 seconds) shows the basic usage of gradescope, which should
explain everything you need to be able to do.

More instruction will be available towards the fall 2020.

Your feedbacks are important for us to improve the teaching and make the learning process more effective and enjoyable.
Here are two ways that you could let me know what your think:
1. You may send me an email.
2. If you want to send me some feedback in an anonymous way, you may fill in the following form:

Not all forms of communication found online are appropriate for an academic community or respectful of others. In this course (and in your professional life that follows), you should practice appropriate etiquette online (``netiquette''). Here are some guidelines:

You should read and follow Rasmussen College's 10 Netiquette guidelines every online students needs to know.
If you need extra accommodations, please contact the instructor as soon as possible.
You are encouraged to login Zoom in time (preferably one or two minutes early) and stay until the end.
During the zoom class session,
- please silence all cell phones and other electronic devices;
- Please do not read email or look at websites, social media, etc;
- please actively participate in the zoom class meeting:
  - You are highly encouraged to ask and answer questions.
  - You should also expect that I randomly pick students to help me solve exercises
    and/or answer specific questions.
  - There will be Zoom Poll from time to time:
    You need to response the questions during Zoom Sessions to justify your active attendance.

Students should familiarize themselves with the Emory College honor code here
- http://catalog.college.emory.edu/academic/policies-regulations/honor-code.html.
Students are encouraged to share ideas and solutions on problem sets and labs, but must
express those ideas in their own words in their submitted work.
Students are not authorized to view or use the work of another student during exams.

Your success in this class is important to me. We will all need accommodations because we all learn differently. If there are aspects of this course that prevent you from learning or exclude you, please let me know as soon as possible. Together we’ll develop strategies to meet both your needs and the requirements of the course.

I encourage you to visit the Office of Accessibility Services (OAS) to determine how you could improve your learning as well. You can register and make a request for services from OAS. In this case, please do inform me of such requests. See the following link for more information:

http://equityandinclusion.emory.edu/access/index.html

According to the Emory University policies: http://policies.emory.edu/1.3

Discriminatory harassment of any kind, whether it is sexual harassment or harassment on
the basis of race, color, religion, ethnic or national origin, gender, genetic
information, age, disability, sexual orientation, gender identity, gender expression,
veteran’s status, or any factor that is a prohibited consideration under applicable law,
by any member of the faculty, staff, administration, student body, a vendor, a contractor,
guest or patron on campus, is prohibited at Emory.

The page is powered by VimWiki.
Both textbook and slides are shared under Creative Common licences (CC BY-NC-SA).

Some announcements

MATH 221: Linear Algebra

2021 Spring, Emory University

Contacts

Course description

Textbook

Coverage

Prerequisite

Learning outcomes

Students obligations

Homework

Midterm tests

Details about Test I

Due dates for homework and tests

Final exam

Attendance

Assessment

Text and slides

Tentative schedule

Gradescope

Feedback

Netiquette

Honor code

Accessibility

Harassment

Some fun links

Acknowledgement