Some announcement:
- You are very welcome to choose this class. For any questions regarding enrollment, please contact Prof. Ettinger: bree.b.ettinger@emory.edu.
- Here is the list of all lecture videos for the whole semester.

- Contacts
- Schedules
- Course description
- Textbook
- Coverage
- Prerequisite
- Learning outcomes
- Students obligations
- Homework
- Midterm tests
- Due dates for homework and tests
- Final exams
- Attendance
- Assessment
- Text and slides
- Tentative schedule
- Gradescope
- Feedback
- Netiquette
- Honor code
- Accessibility
- Harassment
- Some fun links
- Acknowledgement
| Lecture Instructor | Dr. Le Chen |
| le.chen@emory.edu (please include "Math 221" in the subject field) | |
| Office | Math & Science Center - E431 |
| Office hours | Tue, 4:00pm -- 5:00pm, Thur, 2:30pm -- 3:30pm, or by appointments. |
| Zoom Classroom | Click here (password on Canvas page). |
| Lab Instructors | Zitong Pei | Michael Cerchia |
| zitong.pei@emory.edu | michael.cerchia@emory.edu | |
| Sections | 5/7 | 6 |
| Zoom Classroom | Click here (Same password). | Click here (Same password) |
| Sections | Class meeting | Lab (Friday) | Lab Instructor |
|---|---|---|---|
| Math221-5 | Tue: 1:00PM - 2:15PM | 11:20AM - 12:10PM | Zitong Pei |
| Math221-6 | Thu: 1:00PM - 2:15PM | 1:00PM - 1:50PM | Michael Cerchia |
| Math221-7 | Tue: 2:40PM - 3:55PM | 2:40PM - 3:30PM | Zitong Pei |
-
Lectures will be delivered on Tuesday and Thursday. You need to connect to the Zoom class
meeting through the link below (password can be found on Canvas page): - The same link will be used for office hours.
- On Friday, the lab session will be host by the lab instructors:

(Image from Wikipedia)
Linear algebra is a branch of mathematics concerning linear equations such as \(a_1 x_1 + \cdots + a_n x_n = b\), linear maps such as \((x_1,\ldots,x_n) \mapsto a_1x_1 + \cdots + a_n x_n\), and their representations in vector spaces and through matrices. Linear algebra is central to almost all areas of mathematics. It is also used in most sciences and engineering areas.
This course begins with the definition of a matrix and some fundamental operations that can be performed on matrices, such as adding or multiplying two matrices together. Vector spaces are also introduced. A connection is then formed by modeling vector spaces using matrices. Advanced topics involving matrices, such as diagonalization and quadratic forms, eigenvalues and eigenvectors, orthogonalization, and the Gram-Schmidt process are examined. At the end of the class, you will understand how google ranks web pages.
We will use the following online book which is free to download:
- "Linear Algebra with Applications", by W. Keith Nicholson, Version 2019 - Revision A.
-

- | Official website: https://lyryx.com/linear-algebra-applications/ | Download a pdf file |
The book consists of eleven chapters, we will cover most parts of the first eight chapters:
- Chapter 1. Systems of Linear Equations.
- Chapter 2. Matrix Algebra
- Chapter 3. Determinants and Diagonalization
- Chapter 4. Vector Geometry
- Chapter 5. Vector Space \(\mathbb{R}^n\)
- Chapter 6. Vector Spaces
- Chapter 7. Linear Transformations
- Chapter 8. Orthogonality
-
Chapter 9. Change of Basis -
Chapter 10. Inner Product Spaces -
Chapter 11. Canonical Forms
- Six hours of AP BC credit, or
- Math 12 or 112Z
By the end of this course, students will be able to
-
Solve system of linear equations, perform matrix operations, find the inverse of a matrix, check
vectors for linear independence. -
List the vector space properties for \(\mathbb{R}^n\), give examples of subspaces, find bases for
subspaces, find its dimension, find orthogonal bases for subspaces, identify linear
transformations. -
Find eigenvalues and eigenvectors, determinants, characteristic polynomial, perform
diagonalization of a matrix. -
Give examples of vector spaces, check for linear independence, find bases, dimension, identify
linear transformations and find matrix representation for linear transformations.
In order to successfully master the material and complete the course, you are expected to
- Read the textbook and watch video lectures for each section.
- Attend weekly Zoom class meeting and weekly lab session, and watch video recordings for the other weekly class meeting.
- Response to the Zoom poll during the class meeting.
- Participate actively in group activities during Zoom meetings.
- Complete and submit weekly homework through gradescope.
- Read solutions and any feedback you receive for each problem set.
- Complete three midterm tests and one final exam.
- Use appropriate etiquette and treat other students with respect in all discussions.
- Do not hesitate to ask for help whenever needed.
Note: The syllabus was created in May 2020, and it is subject to changes during the semester.
- There will be eleven weekly homework assignments.
- Homework of a week will be usually assigned by the Friday of that week.
- It will be due on the following week on Thursday at 1pm unless announced otherwise.
- No late homework will be accepted.
-
The homework consists of two phases:
- In Phase I, you need to complete questions on Canvas Quiz.
- In Phase II, you need to write details of some problems and upload your solutions to gradescope.
-
Keep in mind that, the Canvas Quiz part, no matter it is for homework, test or final exam, you
will be given two attempts and the latest attempt will be recorded. -
The lowest grade will be dropped, that is, the final score for the homework will be averaged over the rests.
-
Note that the drop policy is not a bonus. It aims at accounting for all circumstances
such as sickness, injuries, family emergencies, religion holidays, etc.
-
Note that the drop policy is not a bonus. It aims at accounting for all circumstances
- There will be three midterm tests in the following three Fridays.
| Date | |
|---|---|
| Test I | 09/04/2020 |
| Test II | 10/02/2020 |
| Test III | 10/30/2020 |
-
Please note down the above three dates. There will be no late exam. In case of time
conflict, please contact the instructor in the first two weeks of the semester. -
The test consists of two phases as the homework. The only difference is that you need to complete
both Phases in 24 hours.
-
Here are a list of due dates for eleven homeworks and three tests (the Phase II part).
Tuesday Thursday Friday Saturday Week 1 08/19 08/21 Week 2 08/25 08/27 HW01 due at 1pm 08/28 Week 3 09/01 09/03 HW02 due at 1pm; RS 09/04 Test I 09/05 Test I due at 6pm Week 4 09/08 09/10 09/11 Week 5 09/15 09/17 HW04 due at 1pm 09/18 Week 6 09/22 09/24 HW05 due at 1pm 09/25 Week 7 09/29 10/01 HW06 due at 1pm; RS 10/02 Test II 10/03 Test II due at 6pm Week 8 10/06 10/08 10/09 Week 9 10/13 10/15 HW08 due at 1pm 10/16 Week 10 10/20 10/22 HW09 due at 1pm 10/23 Week 11 10/27 10/29 HW10 due at 1pm; RS 10/30 Test III 10/31 Test III due at 6pm Week 12 11/03 11/05 11/06 Week 13 11/10 11/12 HW11 due at 1pm 11/13 Week 14 11/17 11/19 RS 11/20 Week 15 11/24 HW12 due at 1pm; RS - RS: review session.
- Final exam will be cumulative.
-
It will be in a similar form as the midterm tests, namely, you will have two phases:
- Phase I: Canvas quiz at the following time slot:
- Tuesday, Dec. 8th, from 6:30-9:00pm (Atlanta local time)
-
There will be 75 points in total with 16 choice problems and 5 points each. One problem is
bonus problem.- Phase II: You will need to upload solutions to Gradescope.
- It will be released on Dec. 8th at 9:00pm
- It will be due on Dec. 9th at 9:00pm
- The total points are 25 points.
- There will be about two proof-based problems.
- The attendance will be collected during Zoom Sessions via Zoom Poll.
- You will need to answer questions during the Zoom sessions actively in order to count your attendance.
-
In case you have time-zone issues or some emergency situations, please contact me
- either at the beginning of the semester for the whole semester;
- or at least one day before the class meeting for a specific Zoom session.
-
The attendance points will be computed as follows
\[
\text{Attendance points} = 100 \times \text{percentage of polls that you respond throughout the semester.}
\]
- The final score will be determined as follows:
-
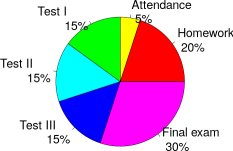
-
Based on the final score (plus potential bonus points), the final letter grade will be determined as follows:
Grade (+) Grade Grade (-) A 92%-100% A- 90%-91.9% B+ 87%-89.9% B 82%-86.9% B- 80%-81.9% C+ 77%-87.9% C 72%-76.9% C- 70%-71.9% D+ 67%-67.9% D 67%-67.9% D- 60%-61.9% F 0%-59.9% - You can download the following spreadsheet to compute your letter Grade.
-
Curving policies: I may make a curve of the grades after the final exam as I have promised. Here
is the slight more detail that how I would do that: You are eligible for grade curving provided
that you did better in the final than the semester average. So do not give up and take the final
exam as a rare opportunity to solidify your knowledge of linear algebra.
- You can download text for each chapter or section below.
- Slides will be updated constantly throughout the semester and please check the time stamp on the front page.
- The application parts of each chapter will be skipped due to lack of time. However, the materials are given for motivated students to study.
| Chapter/Section | Text | Slides | Slides |
|---|---|---|---|
| Chapter 1. Systems of Linear Equations | text | ||
| Section 1-1. Solutions and Elementary Operations | text | presentation | handout |
| Section 1-2. Gaussian Elimination | text | presentation | handout |
| Section 1-3. Homogeneous Equations | text | presentation | handout |
|
|
text | ||
|
|
text | presentation | handout |
|
|
text | presentation | handout |
| Section 1-S. Supplementary Exercises for Chapter 1 | text | ||
| Chapter 2. Matrix Algebra | text | ||
| Section 2-1. Matrix Addition and Scalar Multiplication and Transportation | text | presentation | handout |
| Section 2-2. Matrix-Vector Multiplication | text | presentation | handout |
| Section 2-3. Matrix Multiplication | text | presentation | handout |
| Section 2-4. Matrix Inverses | text | presentation | handout |
| Section 2-5. Elementary Matrices | text | presentation | handout |
| Section 2-6. Linear Transformations | text | presentation | handout |
| Section 2-7. LU-Factorization | text | presentation | handout |
|
|
text | ||
|
|
text | presentation | handout |
| Section 2-S. Supplementary Exercises for Chapter 2 | text | ||
| Chapter 3. Determinants and Diagonalization | text | ||
| Section 3-1. The Cofactor Expansion | text | presentation | handout |
| Section 3-2. Determinants and Matrix Inverses | text | presentation | handout |
| Section 3-3. Diagonalization and Eigenvalues | text | presentation | handout |
|
|
text | presentation | handout |
|
|
text | ||
| Section 3-6. Proof of the Cofactor Expansion Theorem | text | ||
| Section 3-S. Supplementary Exercises for Chapter 3 | text | ||
| Chapter 4. Vector Geometry | text | ||
| Section 4-1. Vectors and Lines | text | presentation | handout |
| Section 4-2. Projections and Planes | text | presentation | handout |
| Section 4-3. More on the Cross Product | text | presentation | handout |
| Section 4-4. Linear Operators on R3 | text | presentation | handout |
|
|
text | ||
| Section 4-S. Supplementary Exercises for Chapter 4 | text | ||
| Chapter 5. Vector Space Rn | text | ||
| Section 5-1. Subspaces and Spanning | text | presentation | handout |
| Section 5-2. Independent and Dimension | text | presentation | handout |
| Section 5-3. Orthogonality | text | presentation | handout |
| Section 5-4. Rank of a Matrix | text | presentation | handout |
| Section 5-5. Similarity and Diagonalization | text | presentation | handout |
|
|
text | ||
|
|
text | ||
| Section 5-S. Supplementary Exercises for Chapter 5 | text | ||
| Chapter 6. Vector Spaces | text | ||
| Section 6-1. Examples and Basic Properties | text | presentation | handout |
| Section 6-2. Subspaces and Spanning Sets | text | presentation | handout |
| Section 6-3. Linear Independence and Dimensions | text | presentation | handout |
| Section 6-4. Finite Dimensional Spaces | text | presentation | handout |
|
|
text | ||
|
|
text | ||
| Section 6-S. Supplementary Exercises for Chapter 6 | text | ||
| Chapter 7. Linear Transformations | text | ||
| Section 7-1. Examples and Elementary Properties | text | presentation | handout |
| Section 7-2. Kernel and Image of a Linear Transformation | text | presentation | handout |
| Section 7-3. Isomorphisms and Composition | text | presentation | handout |
|
|
text | ||
|
|
text | ||
| Chapter 8. Orthogonality | text | ||
| Section 8-1. Orthogonal Complements and Projections | text | presentation | handout |
| Section 8-2. Orthogonal Diagonalization | text | presentation | handout |
| Section 8-3. Positive Definite Matrices | text | presentation | handout |
| Section 8-4. QR-Factorization | text | presentation | handout |
| Section 8-5. Computing Eigenvalues | text | presentation | handout |
| Section 8-6. The Singular Value Decomposition | text | presentation | handout |
|
|
text | ||
|
|
text | ||
|
|
text | ||
|
|
text | ||
|
|
text |
Here is the list of all lecture videos for the whole semester.
-
Below is the tentative schedule that may change during the semester:
Tuesday (lecture) Thursday (lecture) Friday (lab) Week 1 08/19 First class, 1.1 08/21 Week 2 08/25 1.2-1.3 08/27 2.1-2.2 08/28 Week 3 09/01 2.2 - 2.3 09/03 RS 09/04 Test I Week 4 09/08 2.4 09/10 2.5 09/11 Week 5 09/15 2.6-2.7 09/17 3.1 09/18 Week 6 09/22 3.2 09/24 3.3 09/25 Week 7 09/29 RS 10/01 RS 10/02 Test II Week 8 10/06 4.1 10/08 4.2 10/09 4.3 Week 9 10/13 5.1 10/15 5.2 10/16 Week 10 10/20 5.3-5.4 10/22 5.5 10/23 Week 11 10/27 RS 10/29 RS 10/30 Test III Week 12 11/03 6.1-6.2 11/05 6.3(-6.4) 11/06 Week 13 11/10 8.1-8.2 11/12 8.3-8.4 11/13 Week 14 11/17 8.6 11/19 RS 11/20 Week 15 11/24 Last class (RS) - RS: Review Session
-
For students who take synchronized session on Tuesday (resp. Thursday)
- Option 1 (recommended): please timely watch recording for Thursday (resp. Tuesday), which should be available in the same day.
- Option 2 (acceptable): you can also attend the session(s) on Thursday (resp. Tuesday).
-
We will use gradescope to handle submissions of homework, take-home tests and exams,
which allows us to provide fast and accurate feedback on your work. -
As soon as grades are posted, you will be notified immediately so that you can log in and see your
grades and feedback. -
Your Gradescope login is your university email, and your password can be changed there. The same
link can be used if you need to set your password for the first time.- You should have received an email from Gradescope for the registration (sent out on 07/23/2020);
-
If you have not yet received this email, please use the Entry Code to register yourself:
9Y6R48.
- If you have any questions regarding Gradescope, please send your message to
-
Printer+scanner or tablet
-
The easiest way to submit the homework/tests/exams is the following steps:
- print the given template;
- complete the problem sets;
- scan the resulting paper (make sure it is legible);
- upload the scanned file to gradescope.
-
Alternatively, if you have a tablet that you can write on it, you may simply write on the
template pdf file and upload the resulting file.
-
The easiest way to submit the homework/tests/exams is the following steps:
-
The following short video (1 minutes 40 seconds) shows the basic usage of gradescope, which should
explain everything you need to be able to do.
- More instruction will be available towards the fall 2020.
- Your feedbacks are important for us to improve the teaching and make the learning process more effective and enjoyable.
-
Here are two ways that you could let me know what your think:
- You may send me an email.
- If you want to send me some feedback in an anonymous way, you may fill in the following form:
Not all forms of communication found online are appropriate for an academic community or respectful of others. In this course (and in your professional life that follows), you should practice appropriate etiquette online (``netiquette''). Here are some guidelines:
- You should read and follow Rasmussen College's 10 Netiquette guidelines every online students needs to know.
- If you need extra accommodations, please contact the instructor as soon as possible.
- You are encouraged to login Zoom in time (preferably one or two minutes early) and stay until the end.
-
During the zoom class session,
- please silence all cell phones and other electronic devices;
- Please do not read email or look at websites, social media, etc;
-
please actively participate in the zoom class meeting:
- You are highly encouraged to ask and answer questions.
-
You should also expect that I randomly pick students to help me solve exercises
and/or answer specific questions. -
There will be Zoom Poll from time to time:
You need to response the questions during Zoom Sessions to justify your active attendance.
- Students should familiarize themselves with the Emory College honor code here
-
Students are encouraged to share ideas and solutions on problem sets and labs, but must
express those ideas in their own words in their submitted work. - Students are not authorized to view or use the work of another student during exams.
Your success in this class is important to me. We will all need accommodations because we all learn differently. If there are aspects of this course that prevent you from learning or exclude you, please let me know as soon as possible. Together we’ll develop strategies to meet both your needs and the requirements of the course.
I encourage you to visit the Office of Accessibility Services (OAS) to determine how you could improve your learning as well. You can register and make a request for services from OAS. In this case, please do inform me of such requests. See the following link for more information:
- According to the Emory University policies: http://policies.emory.edu/1.3
Discriminatory harassment of any kind, whether it is sexual harassment or harassment on the basis of race, color, religion, ethnic or national origin, gender, genetic information, age, disability, sexual orientation, gender identity, gender expression, veteran’s status, or any factor that is a prohibited consideration under applicable law, by any member of the faculty, staff, administration, student body, a vendor, a contractor, guest or patron on campus, is prohibited at Emory.
- Why study linear algebra?
- Fun Linear Algebra Problems
- An Intuitive Guide to Linear Algebra
- The $25,000,000,000 eigenvectorthe linear algebra behind Google
-
This syllabus is created following some sample syllabuses from my colleagues which
include Mike Carr, Dwight Duffus, Bree Ettinger, Manuela Manetta, James Nagy. - The page is powered by VimWiki.
- Both textbook and slides are shared under Creative Common licences (CC BY-NC-SA).